Examath 8-15 est inclus dans l’abonnement :
Examath 8-15 est inclus dans l’abonnement :
PRÉSENTATION D’EXAMATH 8-15
Examath 8-15 est un logiciel de bilan orthophonique mathématique et test dyscalculie destiné à évaluer les représentations et conduites numériques, le calcul, la résolution de problèmes, le raisonnement verbal et non verbal, le lexique spécifique, chez des enfants du CE2 à la 3ème.
Le Trouble d’apprentissage en mathématique (DSM 5, 2013)
Trouble d’apprentissage en mathématiques= Difficultés d’apprentissage et d’utilisation des capacités académiques *
« La dyscalculie est un autre terme utilisé pour décrire un ensemble de problèmes caractérisés par des difficultés à traiter des données numériques, à apprendre des faits arithmétiques et à réaliser des calculs exacts et fluides. Si le terme de dyscalculie est utilisé pour définir cet ensemble spécifique de difficultés mathématiques, il est important de préciser toute difficulté éventuellement présente telle que des difficultés de raisonnement mathématique ou de raisonnement verbal correct ».
* Sur le plan scientifique, le terme “trouble logico-mathématique” n’est plus reconnu
Objectifs d’Examath
Les atouts
• Des épreuves de test dyscalculie communes pour les élèves du primaire et du collège et d’autres spécifiques selon le niveau scolaire
• Randomisation : liberté de proposer les épreuves sans ordre pré-établi.
• Présentation des résultats ergonomique (graphique général des performances par modules, graphiques et normes pour les résultats principaux, résultats détaillés)
• Résultats imprimables et exportables en version word ou pdf
• Accès permanent aux réponses du patient
• Un univers graphique époustouflant
• Des consignes de passation et de cotation accessibles à tout moment
• Arrêt automatique pour certaines épreuves si trop d’échecs consécutifs
• L’intégration du programme dans l’espace Evaluation de la plateforme HappyNeuron Pro, avec la sauvegarde de vos données patients sur un serveur sécurisé agréé “données de santé” et des mises à jour automatiques
– des modèles de démarche évaluative en fonction de la plainte (difficultés en calcul, difficultés en résolution de problèmes)
– des pistes diagnostiques (dyscalculie primaire/secondaire, trouble du raisonnement mathématique)
– des exemples de démarches diagnostiques à partir de manifestations cliniques
Description de la batterie
40 épreuves (étalonnées sur 5 niveaux) réparties dans 6 modules
Étalonnage
443 enfants et adolescents constituent la cohorte à partir de laquelle les normes statistiques ont été calculées pour les classes suivantes : CE2, CM1, CM2, 6ème-5ème, 4ème-3ème.
La passation des épreuves lors de l’étalonnage a été différenciée selon le niveau scolaire. Certaines épreuves siglées Ⓟ (pour « petits ») n’ont été proposées que pour les plus jeunes, à savoir les CE2, CM1, CM2 ; d’autres siglées Ⓖ (pour « grands) n’ont été proposées qu’aux collégiens. Enfin, un pool commun d’épreuves a été proposé à l’ensemble des sujets quel que soit leur niveau scolaire.
Afin de faciliter l’utilisation ultérieure de cette batterie en pratique clinique, l’administration de la batterie a été pseudo-randomisée : les épreuves ont été présentées aux enfants dans un ordre pseudo-aléatoire et variant à chaque passation. La randomisation d’un test permet d’éviter un effet de fatigabilité qui porterait sur les mêmes épreuves en fin de protocole, ainsi qu’un effet de non-familiarité portant sur les épreuves en début de protocole.
Le temps moyen de passation en pratique clinique est variable selon les enfants et les épreuves proposées, en moyenne autour de 60 minutes.
> Pour en savoir plus sur le contexte théorique, cliquez ici.
A la rentrée, quel étalonnage choisir pour mes bilans Examath 8-15 ?
Découvrez la réponse sur notre blog HappyNeuron en cliquant ici.
Présentation des résultats
Les résultats principaux sont présentés pour chaque épreuve sur les profils-patient par un graphique. Les résultats secondaires sont indiqués sous forme de données textuelles accessibles par un bouton « détails ».
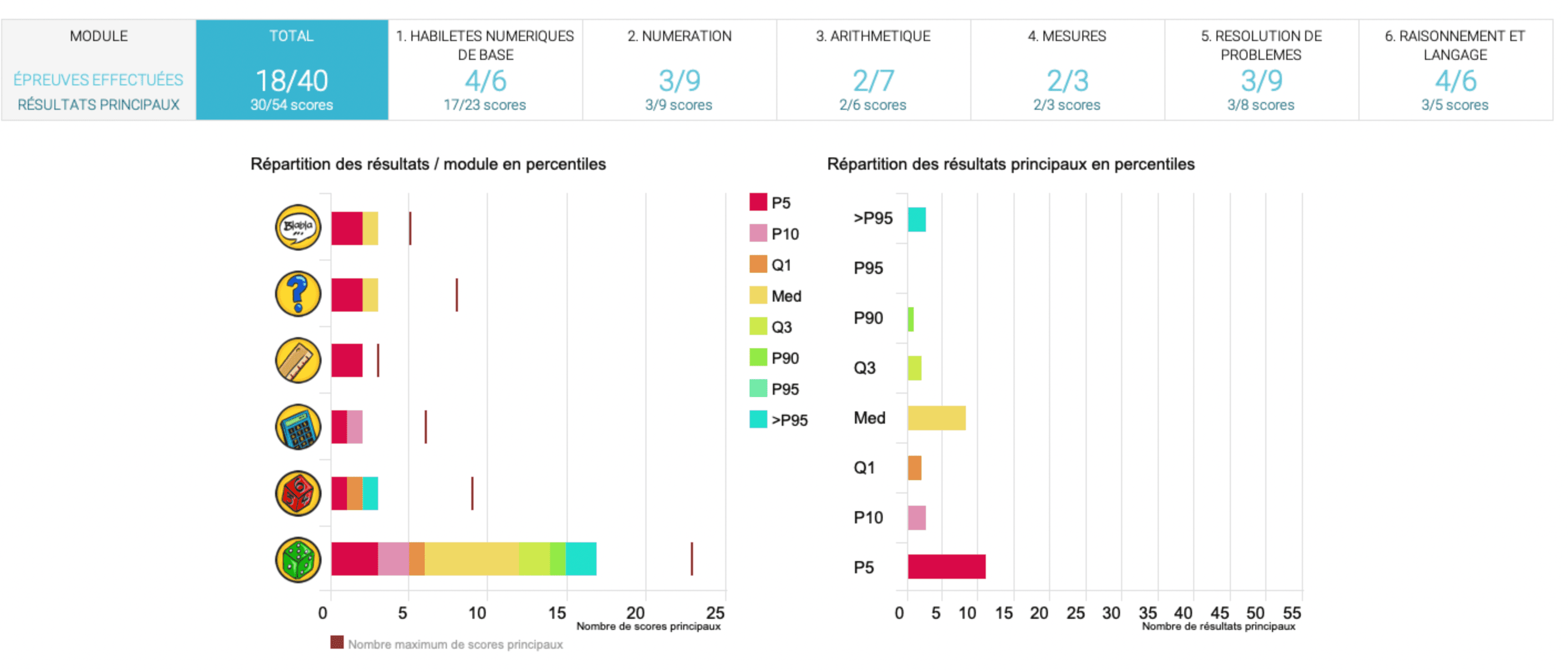
Sur le plan de l’affichage, figurent :
• Le score brut, la valeur de la moyenne, la valeur du seuil pathologique ; la valeur de l’écart-type, le nombre d’écarts-type du patient à la moyenne ;
• La situation en percentiles des résultats du patient au bilan orthophonique mathématique ;
• Un indicateur de normalité de l’échantillon si pertinent : « N ». Pour les séries non gaussiennes, l’interprétation en termes d’écart-type à la moyenne est à effectuer avec prudence, du fait de distributions non homogènes, du degré de dispersion des scores ou des effets de saturation liés à la nature intrinsèque de certaines épreuves. L’analyse en termes de percentiles est à privilégier.
• Un bouton « voir le détail » qui permet pour de nombreuses épreuves d’accéder à des données brutes item par item, ainsi qu’à des scores complémentaires non normés (scores bruts annexes, tableaux ou graphiques récapitulatifs des réponses du patient).
Sur l’interface, est affichée une bande avec dans la case de gauche, le nombre d’épreuves réalisées au total et le nombre de résultats, puis à droite une case par module avec nombre d’épreuves réalisées et nombres de résultats obtenus (il peut y avoir plus d’un résultat par épreuve). Il suffit de cliquer sur une case module pour voir s’afficher tous les résultats principaux par épreuve.
Résultats épreuves d’un module
Module 1 : Habiletés numériques de base
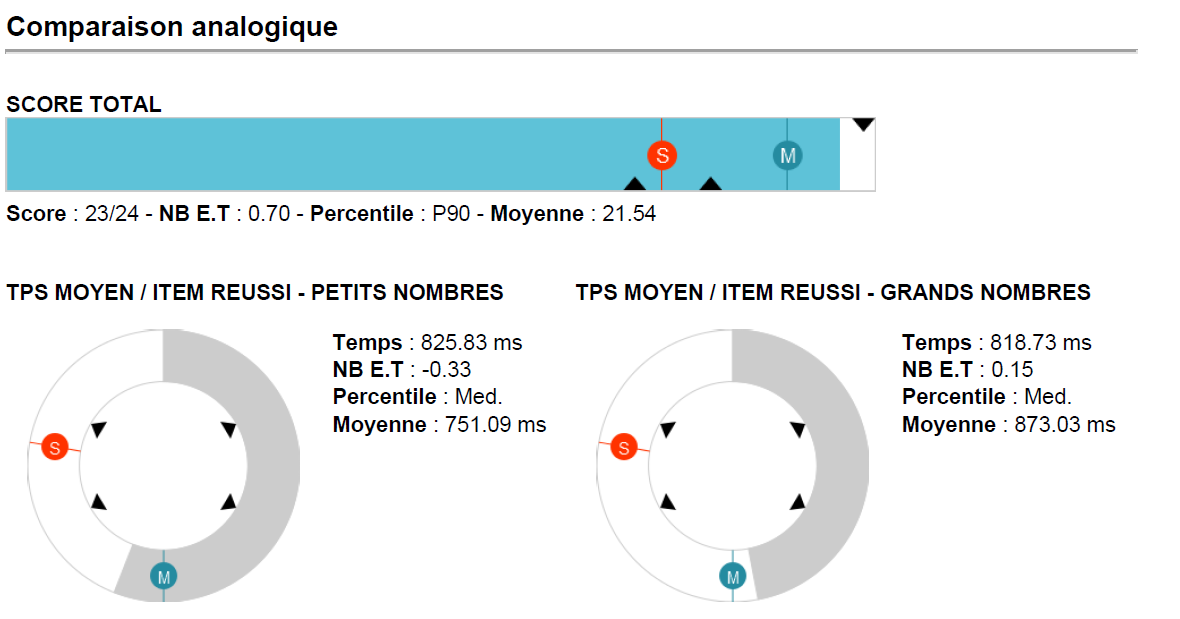
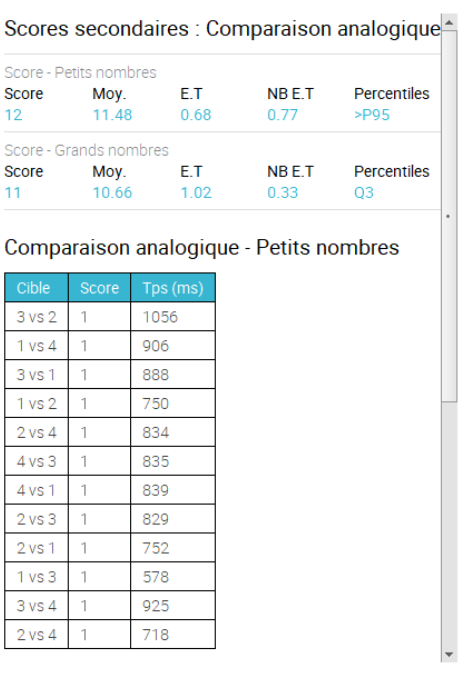
Résultats détaillés
LES AUTEUR(E)S
Marie-Christel Helloin
Orthophoniste
Formatrice et chargée de cours pour le département d’orthophonie de Rouen, Maître de mémoire
Co-auteure de 4 batteries Exalang et de plusieurs logiciels de remédiation
Anne Lafay
Maîtresse de conférences universitaire
Département de psychologie, Université Savoie Mont Blanc
Laboratoire de Psychologie et NeuroCognition – UMR CNRS 5105
Orthophoniste, membre de l’Ordre des Orthophonistes et Audiologistes du Québec
QUESTIONS/RÉPONSES
1. Est-ce qu’Examath 8-15 teste les structures logiques élémentaires (sériation, classification, inclusion etc. ) ?
Non, la batterie s’appuie sur d’autres concepts théoriques et s’intéresse d’abord au traitement du nombre, au calcul et à la résolution de problèmes.
2. Faut-il avoir une formation spécifique pour faire passer cette batterie ?
Il faut être orthophoniste, le manuel se veut aussi formatif, avec des éléments théoriques, des modèles de démarche évaluative, des indications pour l’interprétation qualitative Il est souhaitable de lire le manuel.
3. Pour l’évaluation mathématique, j’ai peur que l’outil informatique ne soit pas adapté car ne permet pas les manipulations
Si la manipulation est un moyen d’intervention utile, intéressant, efficace (voir toutes les études en cognition incarnée par exemple), elle n’est pas absolument nécessaire en évaluation puisqu’il s’agit là de voir si l’enfant / l’adolescent possède, comprend, est capable de manipuler des concepts mathématiques, qui, par essence, sont symboliques la plupart du temps.
4. La passation paraît longue, il y a beaucoup d’épreuves ?
La batterie n’est pas destinée à être passée dans son intégralité. Il faut sélectionner les épreuves selon la plainte.
5. Une amie m’a dit que la passation d’étalonnage avait été très longue
En passation clinique, on ne fait pas tout passer, toutes les épreuves de l’étalonnage n’ont pas été gardées dans chaque niveau.
6. Est ce que je peux faire passer les épreuves des « petits » à des « grands qui auraient beaucoup de difficultés ?
Oui, par contre seules les normes des petits seront disponibles.
7. Est ce que je peux faire passer en plusieurs fois ?
Oui, bien sûr.
8. Est ce que je peux faire passer le test plusieurs fois à un même enfant ?
Oui, bien sûr, il faut alors cliquer sur « nouvelle passation », cela clot la passation précédente.
9. Est ce qu’on peut enregistrer les résultats du patient ?
Les résultats restent stockés, y compris les réponses détaillées du patient dans le programme mais vous pouvez aussi exporter les scores principaux et secondaires en pdf ou en doc Word.
10. Est ce qu’il y aura des formations sur cette batterie ?
Oui, bien sûr.
11. J’ai l’habitude d’utiliser un logiciel de bilan logico-mathématique, quelles sont les différences ?
Il ne s’agit pas ici d’un logiciel de bilan « logico-mathématique », vous ne retrouverez pas a priori les épreuves que vous avez l’habitude d’utiliser mais les approches peuvent être complémentaires selon la plainte du patient, et cette batterie concerne d’abord les plaintes en calcul, numération et résolution de problèmes.
12. Dans quel ordre dois-je faire passer les épreuves ?
Le parcours d’évaluation n’est pas fixe : il dépend de la plainte du patient et des observations que vous faites au fur et à mesure des épreuves. Le chapitre 7 Aide à la Démarche évaluative et diagnostique vous aidera à orienter votre bilan.
Par les mêmes auteures :
1 outil d’évaluation et 2 outils d’intervention
pour les troubles d’apprentissage en mathématiques
Dans la continuité de la batterie Examath 8-15, Examath 5-8, est une nouvelle batterie d’évaluation des habiletés mathématiques à destination des enfants de GSM, de CP et de CE1. Dans un univers graphique attractif pour l’enfant, elle comporte 7 modules et une épreuve courte de dépistage. Examath 5-8 se base sur les modèles théoriques et les données issues de la recherche en psychologie cognitive et psychologie de l’éducation pour les jeunes enfants en début d’apprentissage formel des mathématiques.
Ce programme est centré sur le sens des nombres et cible principalement l’amélioration du système numérique approximatif (SNA). Il permet de stimuler les représentations numériques, ainsi que les capacités en calcul (addition et soustraction) chez les enfants et adolescents. Il permet de travailler le positionnement des nombres symboliques (écrits ou oralisés) sur une ligne horizontale pour aider le patient à mieux se les représenter mentalement. Pour évaluer précisément les progrès du patient, plusieurs lignes de base sont disponibles.
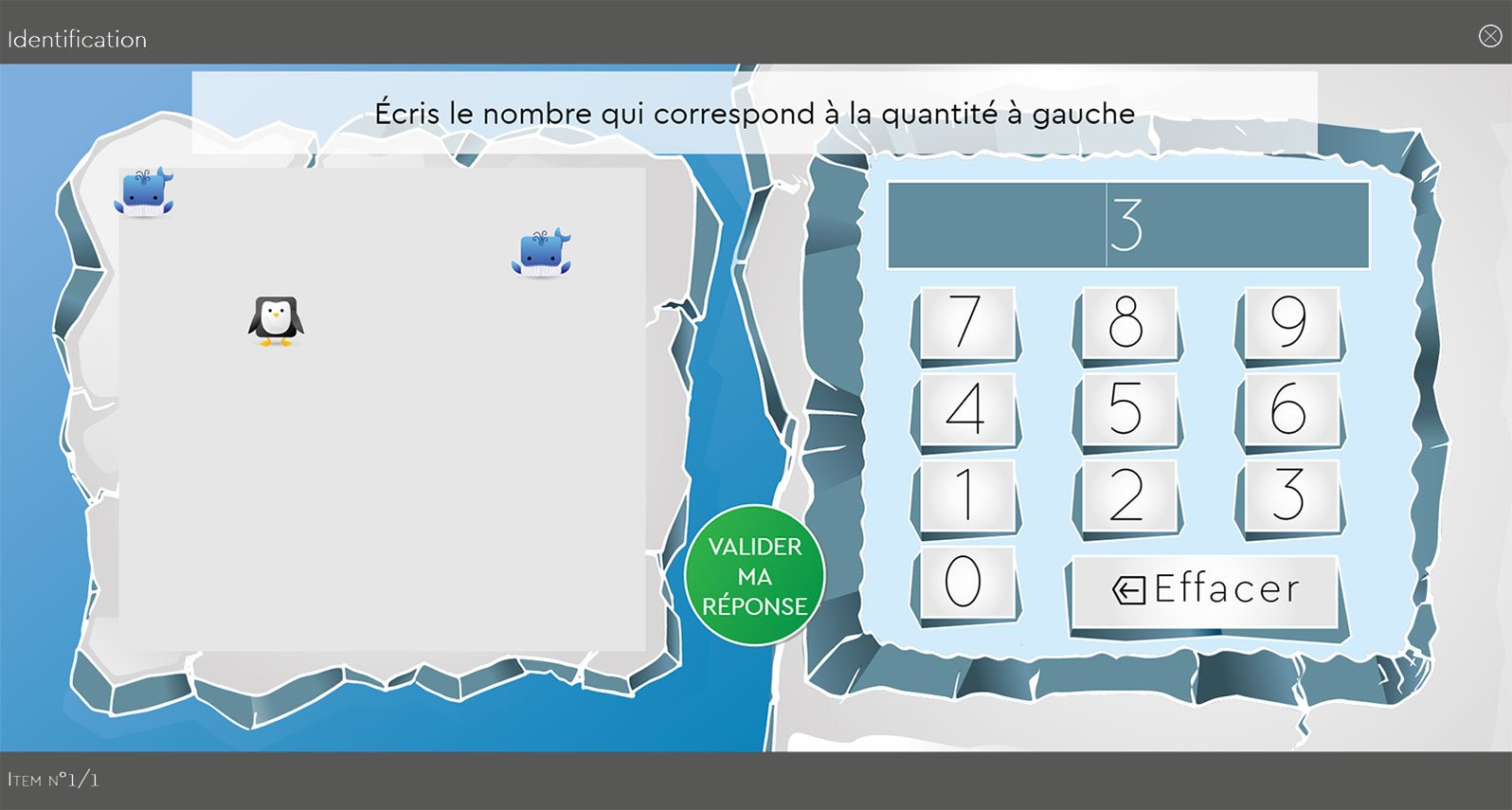
Ce programme est centré le système numérique précis (SNP). Il s’agit de travailler le processus de subitizing acquis par exposition avec les petites quantités, et notamment augmenter la vitesse de traitement. Ce programme vise également la stimulation des compétences en calcul mental. Le patient est amené à réaliser des calculs simples mentaux, en s’appuyant sur la visualisation des petites quantités et sur la décomposition des plus grandes quantités.
Page mise à jour le 03/07/2023
Email : contact@happyneuronpro.com
Tél. : +33.(0)5.61.57.00.71 (numéro non surtaxé,
indicatif +33 depuis l’étranger)
Horaires : 9h30-12h30 et 13h30-17h00
Standard fermé le jeudi matin.
Adresse : Happyneuron
8 bis avenue de la tuilerie
31620 Villeneuve-les-bouloc – France
