Le concept de ligne de base, s’inscrit dans une démarche de preuve basée sur la pratique (ou Practice-Based Evidence) et a vraiment été pensé et développé dans un souci de mesurer rigoureusement l’efficacité de la rééducation.

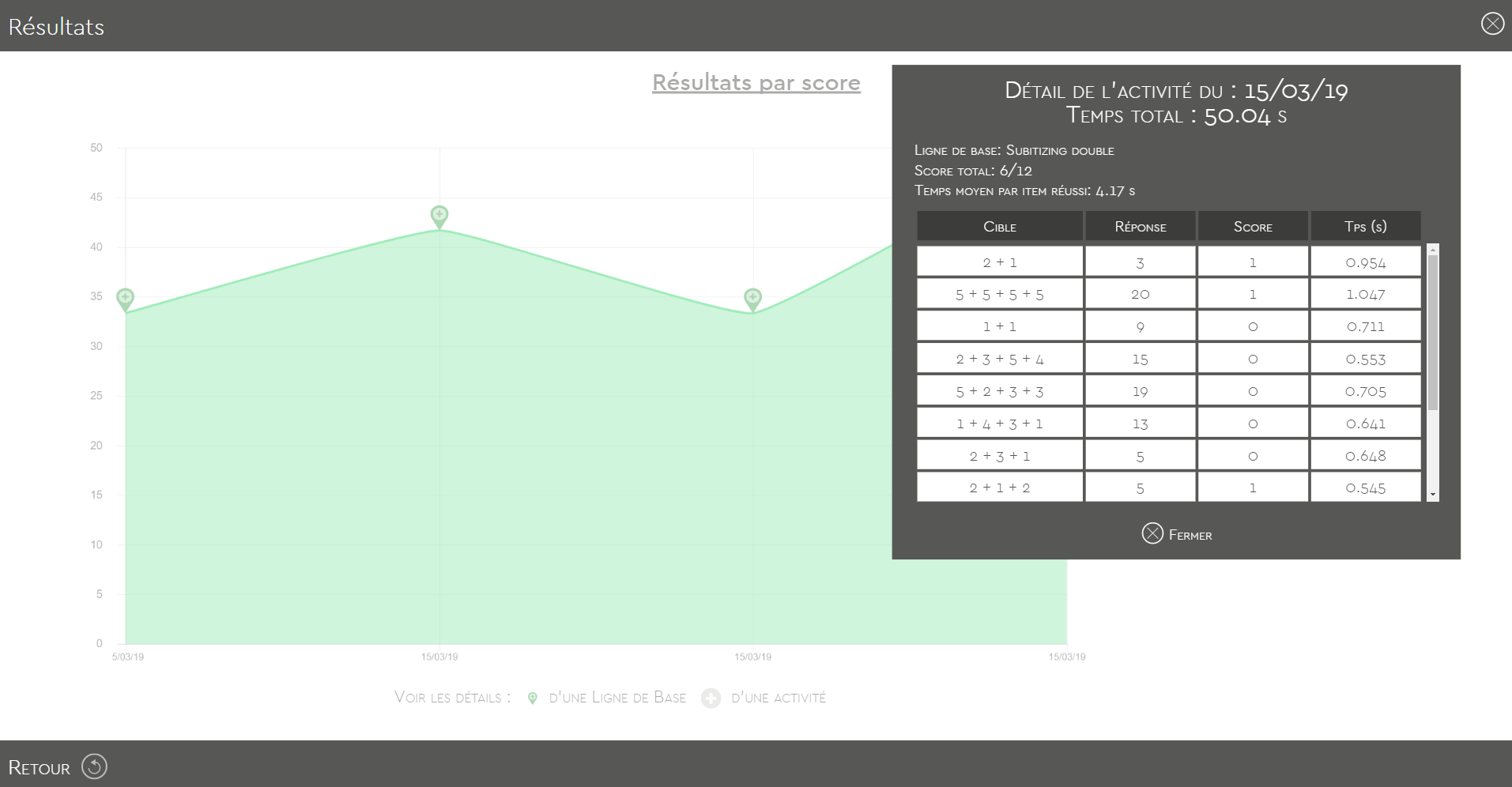
Ainsi, tout comme dans DéCaLigne, afin d’évaluer très précisément les progrès réalisés par le patient, SubéCal vous permet de lui faire passer une série préliminaire destinée à évaluer ses compétences au début de la rééducation. Au fur et à mesure de l’intervention avec SubéCal, vous avez la possibilité de lui refaire passer autant de fois que vous le souhaitez une ligne de base et ainsi constater dans le graphique de progression si les performances de votre patient se sont améliorées. Dans la mesure où il s’agit pour le patient de se perfectionner au niveau du processus, les nombres cibles changent.

INTERVIEW DES AUTEURES DE SUBéCAL

1. Après celui de “ligne numérique”, pourquoi, parmi tous les concepts sur lesquels s’appuie Examath 8-15, avez-vous retenu à présent celui du “subitizing” ?

Parce que le subitizing est reconnu comme une capacité précoce et essentielle dans le développement arithmétique, parce que ce processus a été démontré comme déficitaire chez plusieurs groupes d’enfants ayant un trouble des apprentissages en maths, parce que plusieurs études ont démontré l’efficacité d’un entraînement au subitizing pour améliorer, non seulement le subitizing, mais aussi les habiletés de calcul.

2. SubéCal propose d’évaluer au départ les compétences du patient, avec cette Ligne de base. Pouvez-vous nous expliquer l’intérêt de celle-ci ?

Les lignes de base sont prévues pour évaluer, de manière chiffrée et objective, l’efficacité d’une intervention choisie. Cette démarche permet d’évaluer si le patient s’améliore sur les compétences travaillées et transfert cela à d’autres compétences. Cette démarche permet donc à l’orthophoniste d’évaluer si l’approche d’intervention est efficace, doit être poursuivie ou si une autre approche doit être envisagée.

3. A-t-on besoin de connaître Examath 8-15 (et notamment ses concepts) pour utiliser SubéCal en rééducation ?

Connaitre l’outil Examath 8-15 n’est pas indispensable pour utiliser SubéCal. Une orthophoniste qui aurait évalué les capacités à subitiser et calculer d’un patient avec un tout autre outil pourrait tout à fait utiliser SubéCal pour mener une intervention sur le subitizing et le calcul. En revanche, connaitre la théorie qui sous-tend Examath 8-15 (et donc SubéCal) semble primordial pour comprendre ses enjeux, ses principes et ses objectifs.

4. On entend souvent dire que la manipulation est absolument indispensable en mathématique. Les enfants ne peuvent pas accéder à l’abstraction, passer aux représentations, à partir de “rien”. Mais manipuler virtuellement des objets sur un écran, est-ce la même chose que de les manipuler concrètement ?

Accéder à l’abstraction et aux représentations à partir de “rien” est effectivement difficilement envisageable. L’utilisation d’objets concrets et/ou virtuels de manipulation est une avenue prometteuse pour l’apprentissage immédiat mais aussi pour le maintien des apprentissages et le transfert à d’autres connaissances (voir Bouck et Park, 2018 ; Bouck, Satsangi et Park, 2017 ; Lafay, Osana et Valat, sous presse).

5. Avec quels profils de patients (âge, troubles, pathologies) peut-on utiliser SubéCal ?

SubéCal sera utilisé avec tout patient pour lequel les objectifs d’intervention ciblent l’amélioration de la capacité de subitizing et le calcul mental. SubéCal n’est pas réservé à un âge particulier ; l’orthophoniste pourra choisir un décor enfantin ou un décor neutre par exemple.

6. Les différentes activités de SubéCal peuvent être réalisées en autonomie par le patient. Mais qu’en est-il du rôle du thérapeute dans ce cas ?

SubéCal, malgré tout son potentiel, n’est qu’un outil. L’orthophoniste reste le chef d’orchestre de l’intervention réalisée avec et pour le patient. Il détermine les objectifs d’intervention et les moyens. Il détermine les lignes de base à réaliser en fonction des objectifs d’intervention ciblés ainsi que les exercices, les paramètres, le dosage (nombre de minutes, de séances, fréquence des séances, etc.) qu’il juge le plus adéquat pour son patient. Il ajuste aussi cela grâce à l’analyse des résultats et de la progression observés.

7. Enfin nous ne pouvons pas finir cet interview sans vous poser la question : la suite d’Examath, c’est pour quand ?

Nous travaillons à un Examath 5-8 réservé aux jeunes enfants de Grande section de maternelle au CE1. La conception théorique est bientôt achevée. La conception technique commencera dans le courant de l’année 2019.